U najnovijem broju časopisa Nature Physics objavljen je znanstveni rad naslovljen Sub-symmetry-protected topological states. Rad je objavljen u suradnji Daria Jukića sa Građevinskog fakulteta i Hrvoja Buljana sa Prirodoslovno-matematičkog fakulteta Sveučilišta u Zagrebu te njihovih suradnika u grupi Zhigang Chena sa Sveučilišta Nankai u Kini i Roberta Morandottija sa INRS u Kanadi. Oni su pokazali da u topološkim sustavima koje štiti simetrija, zaštita topoloških rubnih stanja vrijedi čak i kad je simetrija narušena, ako je zadovoljen blaži uvjet odnosno sub-simetrija.
Sub-simetrija znači da simetrija vrijedi samo u jednom dijelu Hilbertovog prostora. Time je promijenjena paradigma vezana za zaštitu rubnih stanja u topološkim sustavima, jer je uvriježeno mišljenje bilo da simetrija u potpunosti mora biti zadovoljena za zaštitu rubnih stanja.
Ovaj rad iz fizike je blisko povezan s matematičkom disciplinom topologijom, koja grubo rečeno proučava geometrijske objekte invarijantne na kontinuirane deformacije, pa je tako torus topološki istovjetan šalici za kavu kao što je prikazano na slici ispod.

Ova se istovjetnost može kvantificirati. Jedan od najpoznatijih rezultata u tom smjeru je Gauss-Bonet teorem koji povezuje lokalnu zakrivljenost neke površine (mnogostrukosti) sa njenim topološkim obilježjima koje karakterizira topološka invarijanta – u slučaju gore to je Eulerova karakteristika koja iznosi 2 za loptu i sve objekte koje kontinuiranim deformacijama izvedemo iz lopte bez da polomimo površinu ili da spojimo dva kraja; za šalicu i torus Eulerova karakteristika je nula (npr. vidi https://en.wikipedia.org/wiki/Gauss%E2%80%93Bonnet_theorem). Topološka invarijanta je kvantizirana nelokalna veličina, a ovim je teoremom povezana s lokalnom veličinom zakrivljenosti površine.
U kvantnoj fizici, topološka kvantna materija predstavlja novu klasu materijala koje karakteriziraju nelokalna topološka svojstva koja proizlaze iz lokalnih (mikroskopskih) stupnjeva slobode. Topološke invarijante mogu biti definirane i na apstraktnim mnogostrukostima, ima ih raznih vrsta poput Chernovog broja kod kvantnog Hallovog efekta, no princip je sličan gore navedenom Gauss-Bonet teoremu.
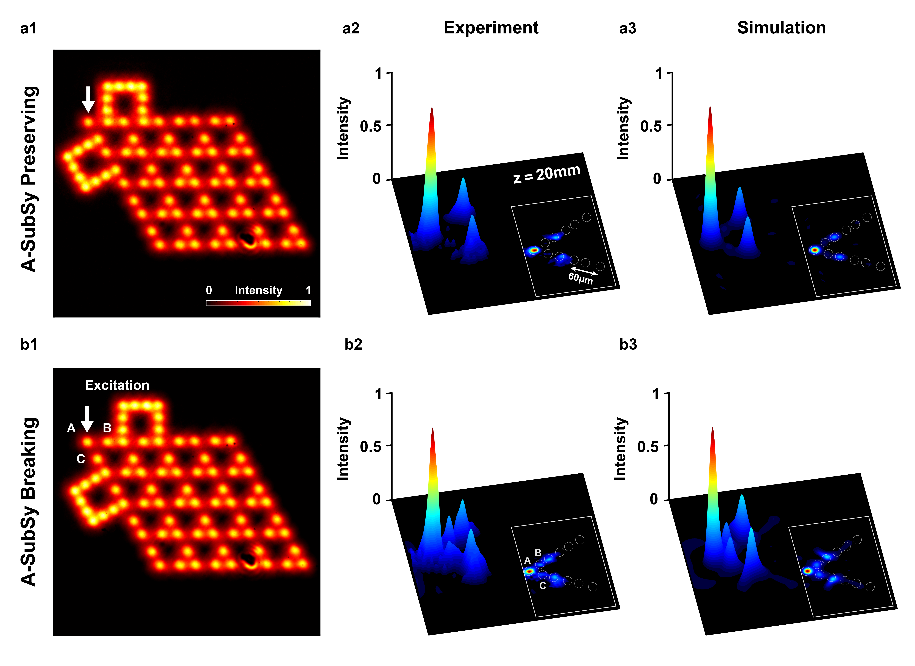
Topološka stanja materija koje štiti simetrija su podskup topoloških materijala gdje bilo koja perturbacija sustava, ako zadovoljava određenu simetriju, neće promijeniti topološku invarijantu i topološki zaštićena rubna stanja koja karakteriziraju takve materijale. Barem je to bila paradigma do ovog rada koji je tu sliku malo izmijenio. Naime, Jukić, Buljan i koautori su pokazali da je za potpunu zaštitu rubnih stanja dovoljno da perturbacije poštuju takozvanu sub-simetriju, a ne cjelokupnu simetriju sustava. Kod sub-simetrije je dovoljno da simetrija vrijedi samo u jednom dijelu Hilbertovog prostora a ne svugdje. Rad je to pokazao teorijski i eksperimentalno. Na slici dolje je primjer perturbacije u Kagome rešetci koja čuva ili lomi sub-simetriju, pa time čuva ili perturbira topološko rubno stanje.
Članak je dostupan na poveznici: https://www.nature.com/articles/s41567-023-02011-9