U članku objavljenom u časopisu Physical Review B, F. Lunić, M. Todorić, B. Klajn, T. Dubček, D. Jukić i H. Buljan izložili su teorijski model za sintetičke anyone u neinteragirajućem mnogočestičnom sustavu. Model se sastoji od neinteragirajćih elektrona na dvodimenzionalnoj ravnini pod utjecajem okomitog homogenong magnetnog polja te proizvoljnog broja okomito položenih tankih zavojnica koje nose određeni dodatni magnetski tok. Pokazano je da pri zamjenama položaja zavojnica sustav nakuplja fazu koja odražava frakcionalnu (anyonsku) statistiku povezanu s vrijednošću dodatnog toka po zavojnici.
U uobičajenim slučajevima (tri dimenzije), kvantna fizika dozvoljava postojanje dvije vrste čestica - bozoni i fermioni. Razlika je u fazi (kut u kompleksnoj ravnini) koju valna funkcija (matematički opis stanja sustava) nakuplja pri zamjeni dvaju identičnih čestica. Ova faza je za bozone 0, a za fermione Pi, što uzrokuje različito statističko ponašanje. Zajedničko u oba slučaja je da dvostruka zamjena ostavlja valnu funkciju nepromijenjenom. U dvije dimenzije, dozvoljene su i čestice čija je statistička faza između ove dvije vrijednosti - Abelovi anyoni, te ne-Abelovi anyoni čije ponašanje je još kompleksnije.
Potencijalna primjena ne-Abelovih anyona kao platforme za topološka kvantna računala čini eksperimentalnu realizaciju i manipulaciju anyona važnim područjem istraživanja. Većina teorijskih prijedloga i eksperimenata dosad bila je u jako interagirajućim sustavima kao što je frakcionalni kvantni Hallov efekt (FQHE). Autori u ovom radu predlažu sintetizaciju Abelovih anyona u jednostavnijim, slabo interagirajućim sustavima kao što je integralni kvantni Hallov efekt pomoću lokalnih probi (u ovom slučaju zavojnica).
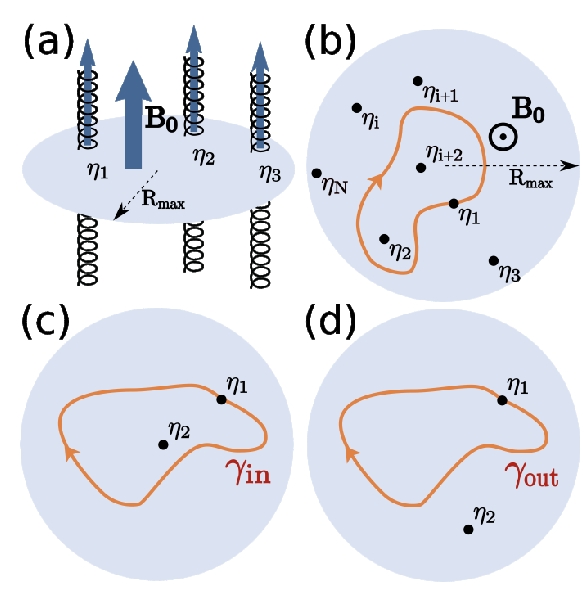
Kako bi se izračunala statistička faza pri adijabatskom obilasku jedne zavojnice oko druge (proces koji po bitnim karakteristikama odgovara dvostrukoj zamjeni), prvo je analitički i numerički pronađeno stanje najniže energije elektronskog sustava takvo da je popunjen samo najniži Landauov level, te su potom izračunate Berryjeve faza koje se nakupljaju kad zavojnica obilazi putanju koja obuhvaća jednu (c) te nijednu (d) identičnu zavojnicu. Razlika faza u ta dva slučaja odgovara statističkoj fazi i njena vrijednost odražava anyonsku statistiku u koodrinatama zavojnica. Nadalje, u radu se diskutira razlika u interpretaciji sintetičkih anyona u odnosu na frakcionalne emergentne kvazičestice u konvencionalnim sustavima (npr. u FQHE), te njene posljedice. Za kraj, autori se dotiču izazova eksperimentalne realizacije modela.
Rad je dostupan na https://journals.aps.org/prb/abstract/10.1103/PhysRevB.101.115139